7444. Игра на графе

Задан граф с 2n вершинами и m ребрами. На каждой вершине и на каждом ребре записано одно целое число. Серик и Жомарт слонялись без дела и придумали новую игру на графе. Правила этой игры следующие:

· Серик начинает игру, после чего ребята ходят по очереди.

· Каждый игрок совершает в точности n ходов.

· На каждом ходе Игрок должен выбрать еще не выбранную ранее вершину.

· Счет Игрока равен сумме чисел, записанных на выбранных им вершинах плюс сумма чисел на ребрах, соединяющих его выбранные вершины.

· Каждый из игроков старается максимизировать разность своего счета и счета оппонента.

· Конечно же, Серик и Жомарт достаточно умны.

Вход. Первая строка содержит целые числа n, m (1 ≤ n, m ≤ 10⁵).

Вторая строка содержит целые числа a₁, a₂, . . . , a_2n (1 ≤ a_i ≤ 1000) – числа на вершинах.

Каждая из следующих m строк содержит три целых числа u, v, w (1 ≤ u, v ≤ n, 1 ≤ w ≤ 1000) – вершины u и v соединены ребром, w – число на этом ребре. Граф не содержит петель.

Выход. Вывести разницу между счетом Серика и Жомарта.

Пример входа	Пример выхода
3 3 2 3 2 2 3 1 6 1 3 4 3 2 1 2 1	1

РЕШЕНИЕ

жадность

Анализ алгоритма

Пусть исходный граф содержит ребро (u, v) весом w, причем на вершинах записаны числа a_u и a_v:

Построим новый граф, в котором каждое такое ребро будет заменено на

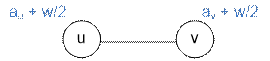
Вес ребра мы перенесли на веса вершин. Если Серик и Жомарт станут играть на новом графе, то разница между счетом при оптимальной игре будет такой же как и на исходном графе. Действительно, если вершину u выберет один из ребят, а вершину v второй, то разница между числом полученных очков останется прежняя:

(a_v + w / 2) – (a_u + w / 2) = a_v – a_u

Если обе вершины выберет один из участников игры, то он получит

(a_v + w / 2) + (a_u + w / 2) = a_v + a_u + w

очков. То есть получит числа приписанные вершинам на исходном графе плюс вес ребра.

Оптимальная игра на новом графе – жадность. Каждый из участников на своем ходу должен выбирать вершину с максимальным приписанным к ней значением.

Пример

Рассмотрим граф, приведенный в примере. Построим для него новый граф.

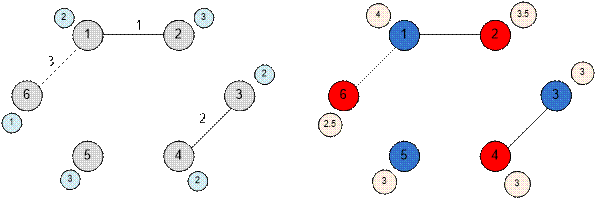
Первый игрок выберет вершины: 1, 3, 5 с весом 4 + 3 + 3 = 10.

Второй игрок выберет вершины: 2, 4, 6 с весом 3.5 + 3 + 2.5 = 9.

Разница между счетом Серика и Жомарта равна 10 – 9 = 1.

Реализация алгоритма

Числа на вершинах графа храним в массиве а.

#define MAX 200001

double a[MAX];

Читаем входные данные.

scanf("%d %d", &n, &m);

n += n;

for (i = 1; i <= n; i++)

scanf("%lf", &a[i]);

Строим новый граф.

for (i = 1; i <= m; i++)

{

scanf("%d %d %d", &u, &v, &w);

a[u] += w / 2.0;

a[v] += w / 2.0;

}

Сортируем массив а по убыванию.

sort(a + 1, a + n + 1, greater<double>());

Моделируем игру – на каждом ходе участник выбирает вершину с максимальным значением.

double res = 0;

for (i = 1; i <= n; i++)

if (i & 1) res += a[i];

else res -= a[i];

Выводим ответ.

printf("%lld\n", (long long)res);